What makes an AI system good at math? Not uncooked computational energy, however one thing that appears virtually contradictory: being neurotically cautious about being proper.
When AI researchers speak about mathematical reasoning, they usually concentrate on scaling up — greater fashions, extra parameters, and bigger datasets. However in apply, mathematical potential isn’t about how a lot compute you’ve to your mannequin. It’s truly about whether or not machines can be taught to confirm their very own work, as a result of at the least 90% of reasoning errors come from fashions confidently stating flawed intermediate steps.
I assume this sounds apparent when you perceive it. Any mathematician would inform you that the important thing to fixing onerous issues isn’t uncooked intelligence — it’s methodical verification. But for years, AI researchers have been attempting to brute-force mathematical potential by making fashions greater, as if sheer computational energy alone would produce cautious reasoning.
Microsoft’s rStar-Math (the highest AImodels.fyi question-answering paper this week) adjustments this sample via three linked improvements: code verification of every reasoning step, a desire mannequin that learns to judge intermediate pondering, and a multi-round self-evolution course of. Their 7B parameter mannequin — utilizing these strategies — matches or exceeds the efficiency of fashions 100 occasions bigger.
The system works by forcing express verification at each step. Each bit of mathematical reasoning have to be expressed as executable code that both runs accurately or fails. This creates a form of synthetic doubt, which serves as a wholesome skepticism that stops unjustified leaps. However verification alone isn’t sufficient, and the system additionally must be taught which reasoning approaches work higher than others, which it does via its desire mannequin. And it wants to enhance over time, which it achieves via a number of rounds of self-training.
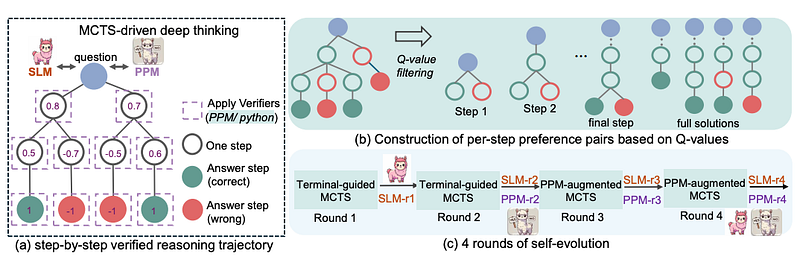Overview of rStar-math. Be aware the verified reasoning trajectory module. - Every reasoning step is expressed as a brief snippet of Python code that should run accurately.
- A “course of desire mannequin” charges every step.
- The system goes via a number of rounds of coaching, the place every iteration builds on the verified options from the final one.
I believe that this fixed suggestions loop forces the smaller mannequin to “suppose out loud” in verifiable steps quite than merely guessing. This matches a sample we’re seeing throughout the ML world proper now, specializing in efficiency positive factors via chain-of-thought patterns. OpenAI’s o1 is essentially the most salient instance of this, however I’ve coated plenty of different papers that take a look at comparable approaches.
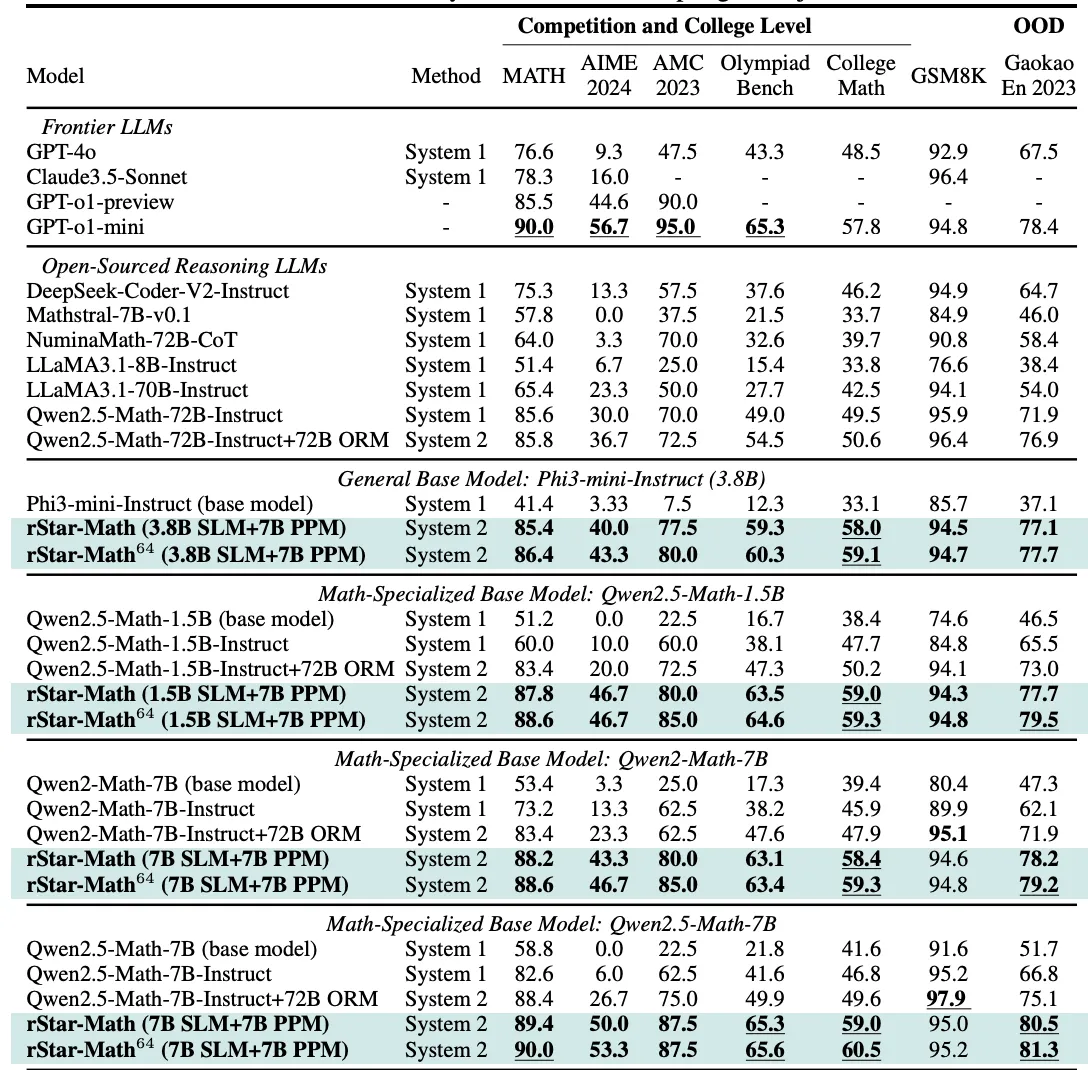
Desk 5: The outcomes of rStar-Math and different frontier LLMs on essentially the most difficult math benchmarks. rStar-Math64 reveals the Cross@1 accuracy achieved when sampling 64 trajectories.” — from the paper.
Anyway, by the ultimate spherical, this smaller mannequin apparently scores 90% on the MATH benchmark and solves 53% of actual Olympiad-level AIME issues — sufficient to put it within the prime 20% of human contestants. I might have anticipated outcomes like this to require a mannequin with way more parameters. However rStar-Math means that greater isn’t all the time higher if the system can confirm every step and reject defective paths early.
What’s thrilling to me is how this may generalize. For math, code execution is a clear verification sign: both the code runs accurately, and the outputs line up with the partial end result, or it doesn’t. In different domains — like regulation, vaccine analysis, or inventive artwork duties — there isn’t an apparent sure/no check for each step. Nonetheless, I think about we may nonetheless create domain-specific checks or desire fashions that determine whether or not each bit of reasoning is dependable. In that case, smaller fashions may compete with and even surpass bigger ones in lots of specialised duties so long as every reasoning step will get validated.
Some may fear that code-based verification is restricted and possibly ask, “How can we scale that to each downside?” However I believe we’ll see inventive expansions of this method. For instance, a authorized mannequin may parse related statutes or check arguments in opposition to identified precedents, and a medical mannequin may seek the advice of a data base or run simulations of normal remedies. We may even apply these concepts to on a regular basis duties so long as we construct strong checks for correctness.
The place else are you able to see this method being helpful? Let me know within the feedback. I’d love to listen to what you must say.
